Последние два месяца хорошенечко подсел на ChatGPT. Сделал с помощью него (неё?) два пет-проекта: теле-чат для столовой на работе и расширение для Unity. Оба раза это был удивительный опыт и не потому что «о вау, AI пишет код». Небольшие скрипты я и раньше делал с ChatGPT, что оно пишет работоспособный код — это понятно. Меня удивил весь пользовательский опыт вокруг.
В какой-то момент начинает казаться, что ты на самом деле переписываешься с разработчиком на фрилансе. Не нужен никакой промпт-инжиниринг и не нужно напоминать контекст. Ты просто общаешься с очень вежливым, неунывающим и несдающимся специалистом.
Сейчас я плачу за подписку. До того, после превышения какого-то лимита, ChatGPT переходил на предыдущую версию модели, которая поглупее. Тогда-то и проступает разница. Предыдущая модель как раз-таки неудивительная: не понимает контекст, отвечает сухо — всё ощущение работы с настоящим разработчиком улетучивается. Код-то всё ещё рабочий, а вот опыт уже не тот.
Мой диалог в ChatGPT в среднем выглядит вот так.
Здесь нет фокусов с промптами — я просто общаюсь так, как общался бы с коллегой. Более того, эпольная вежливость ChatGPT настраивает на аналогичное настроение. Кайфую от того, что этот специалист резюмирует твой запрос в начале сообщение и только потом пишет код. Оно тебя сразу подкупает: да да, как бы косноязыко ты не выражался, я тебя понимаю, вот, смотри, что ты хочешь на самом деле…
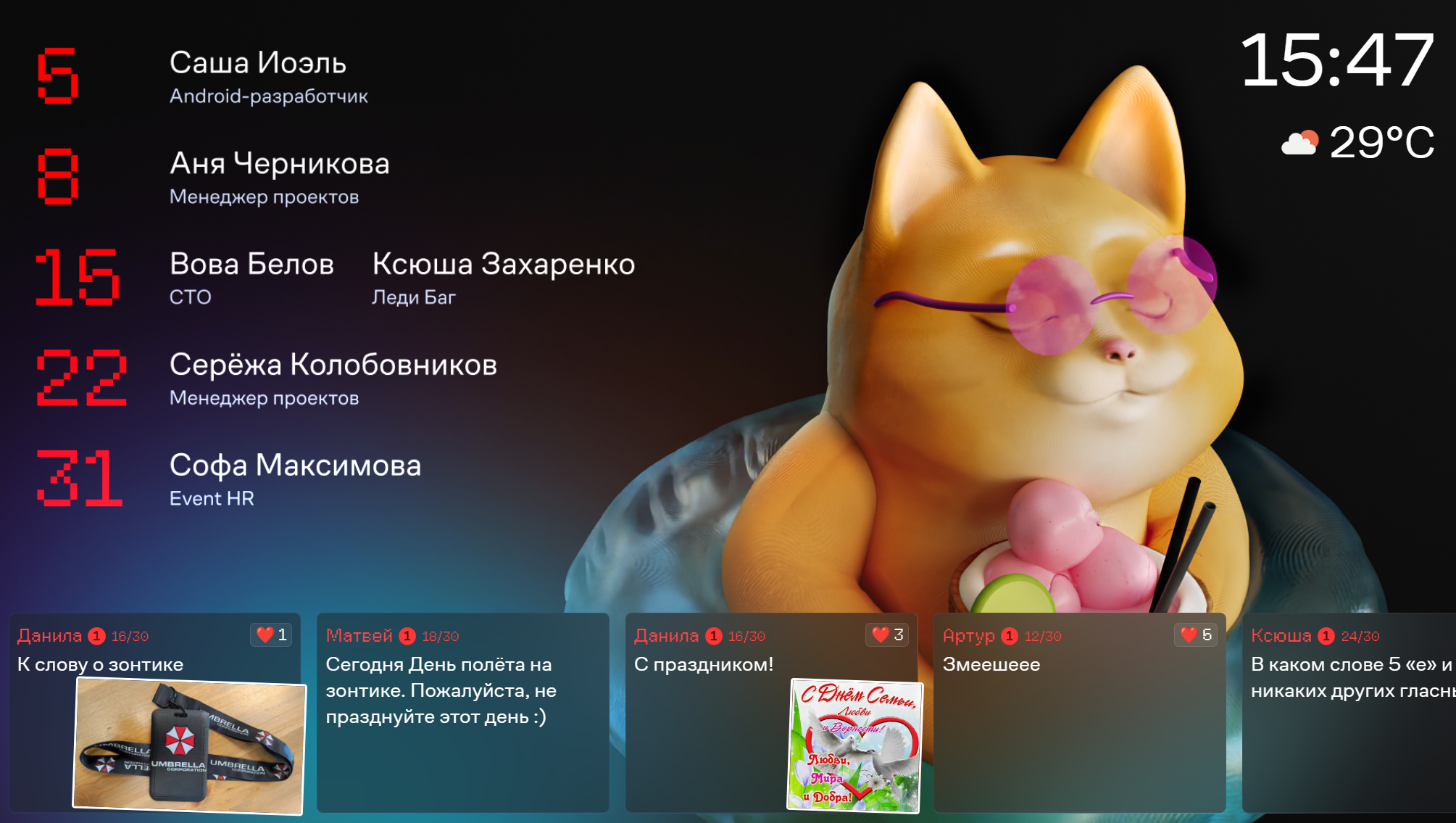
Так вот, те два проекта, для которых я нанял ChatGPT. Первый — теле-чат для столовой. Я хотел, чтобы коллеги могли писать боту в Телеграм и эти сообщения отображались бы на телевизоре. Что-то типа полуночных чатов на ТВ. Вот оно, внизу.
Тут почти весь код написан ChatGPT. Бот принимает сообщение и складывает в Гугл Таблицу. Около ников видно ранг (у всех пока «1») и лайки. Ранг зависит от количества написанных сообщений и лайков к ним. Писать формулы в Гугл Таблице для подсчёта такого уж точно стоит доверить AI, а то там больно своеобразный синтаксис.
В этой работе я увидел главное преимущество ChatGPT для себя. У меня есть какой-никакой опыт в программировании: само по себе составление алгоритма и написание кода — не такая уж и проблема. Проблема — это всё что до этого. Настройка среды для бота, работа с OAuth, автоматизация запуска скриптов при включении сервера… Вот эта вся бюрократия, которая не является программированием как таковым — вот она встаёт блокером для создания продукта. Я рад бы писать код, я просто не знаю куда. И именно эту рутину ChatGPT прекрасно закрывает. Оно подскажет все промежуточные шаги, чтобы ты уже мог наконец открыть заветный файл, куда будешь писать скрипт. А уж писать код самим или с помощью AI это уже проза — и то, и то весело.
Второй пет-проект — расширение для Unity.
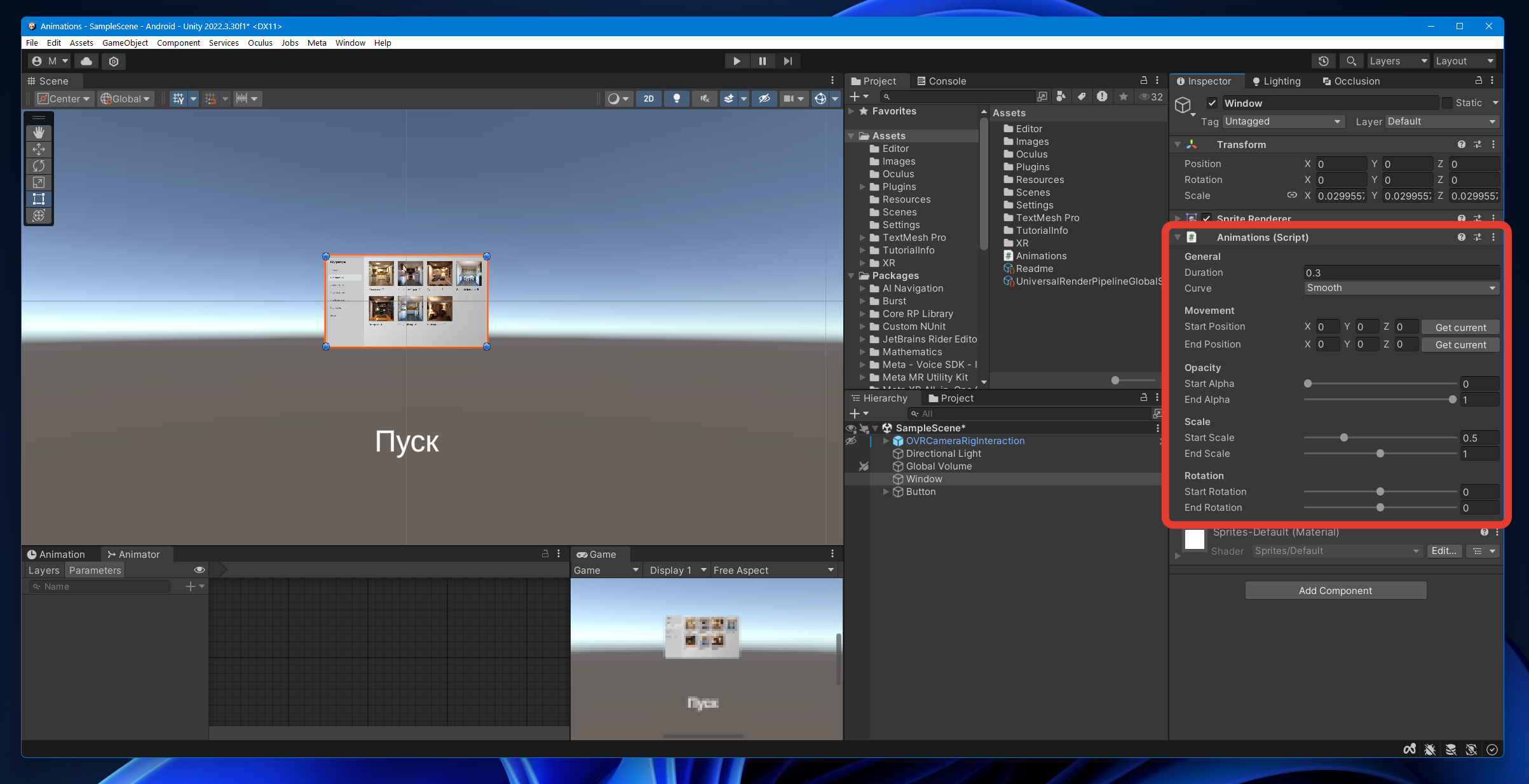
Лонг-стори-шорт: я сейчас увлёкся прототипированием интерфейсов под VR. Это удобнее всего делать в Unity, но в нём тяжело делать именно интерфейсные анимации. Там есть работа со стейт-машиной через Animator, но это больно уж суровый комбайн для моих простых нужд: плавно скрыть или увеличить кнопочку.
У Unity есть моя любимая черта хороших редакторов — он станок, готовый для допилки под нужды мастера. Можно написать скрипт, самим сделать ему интерфейс и просто закидывать как модуль к другим объектам. Мне нужен был инструмент, который позволяет указать начальное и конечное состояние для базовых модификаций элементов интерфейса: двигать, прозрачить, масштабировать и крутить. Конечно же можно управлять длительностью анимации и кривой ускорения.
Запрос достаточно нестандартный. Я не был уверен, что ChatGPT справится. Тут и C#, и всякая внутрянка Unity как среды разработки. Лучше всего работа с AI спорится, когда просишь какую-то простую функцию и потом, шаг за шагом, усложняешь этот код. Так был сделан тот теле-чат. В случае с Unity таки решил пойти ва-банк: прям вот сразу написал ChatGPT весь требуемый функционал. Словно я менеджер, который просто рассказывает лиду, как-что должно работать и в каком виде. В общем — всё сработало с первого раза.
Тогда я понял, что если ты человек с хорошей идеей и базовыми навыками кода (это всё ещё нужно, чтобы нормально объяснить требования и понять результат), у тебя больше нет лимитов — ты можешь собрать любой проект.